 Now, w.l.o.g., let’s consider the 50th value of the estimated local
level. Koopman and Harvey (2003) showed that the smoothed estimates can
be represented as:
Now, w.l.o.g., let’s consider the 50th value of the estimated local
level. Koopman and Harvey (2003) showed that the smoothed estimates can
be represented as:wex is an R package designed to compute the exact
observation weights for the Kalman filter and smoother using the method
described in Koopman and Harvey (2003). It offers an in-depth
exploration of state-space models, enabling researchers and
practitioners to extract valuable insights from their time series data.
This functionality is particularly useful in dynamic factor models,
where the weights can be employed to decompose the contributions of
individual variables to the latent factors (see Example 2 below).
You can install the development version of wex from GitHub with:
# install.packages("devtools")
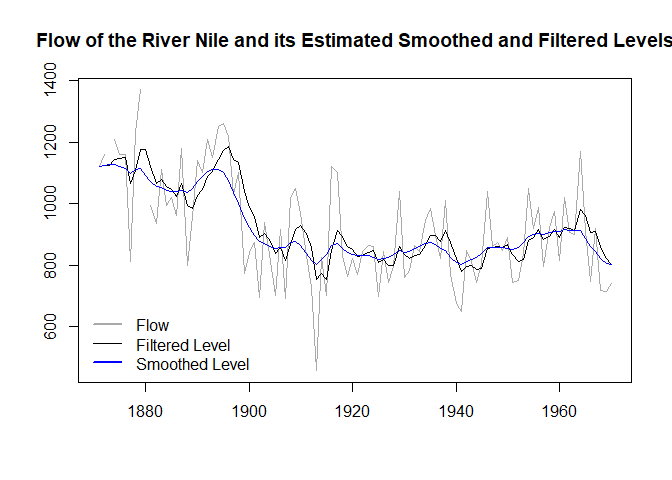
devtools::install_github("timginker/wex")In this illustrative example, we fit the local level model to the Nile dataset and compute the associated smoothed and filtered values.
The resulting estimates are presented in the plot below:
 Now, w.l.o.g., let’s consider the 50th value of the estimated local
level. Koopman and Harvey (2003) showed that the smoothed estimates can
be represented as:
Now, w.l.o.g., let’s consider the 50th value of the estimated local
level. Koopman and Harvey (2003) showed that the smoothed estimates can
be represented as:
$$
\alpha _{t|T}=\sum_{j=1}^{T}w_{j}(\alpha _{t|T})y_{j}.
$$Similarly, the filtered estimated can be computed as:
$$
\alpha _{t|t}=\sum_{j=1}^{t}w_{j}(\alpha _{t|Tt})y_{j}.
$$We can compute the weight of each observation using the
wex function, and compare the local level estimates
obtained from the weighted average of the observed data with the
associated estimates obtained from the Kalman filter and smoother.
wts <- wex(Tt=matrix(1),
Zt=matrix(1),
HHt = matrix(1385.066),
GGt = matrix(15124.13),
yt = t(y),
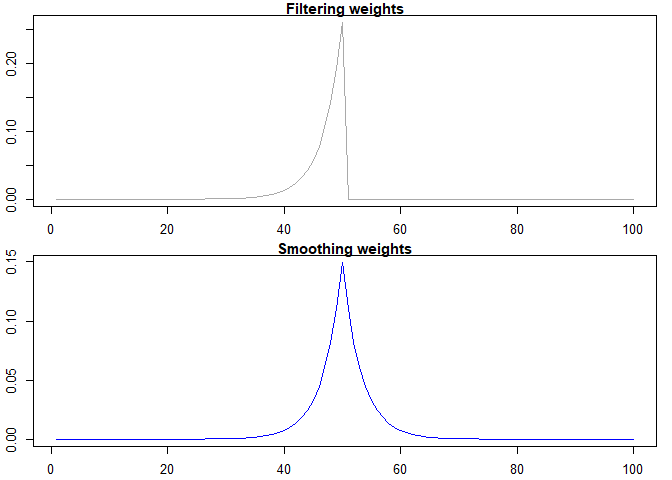
t=50)We can also visualize the weights assigned to each observation:
par(mfrow = c(2, 1),
mar = c(2.2, 2.2, 1, 1),
cex = 0.8)
plot(
wts$Wt,
col = "darkgrey",
xlab = "",
ylab = "",
lwd = 1.5,
type="l",
main="Filtering weights"
)
plot(
wts$WtT,
col = "blue",
xlab = "",
ylab = " ",
lwd = 1.5,
type="l",
main="Smoothing weights"
)
It is also easy to verify the identity between the smoothed and filtered levels obtained from the Kalman filter and the corresponding estimates computed using the weights.
cat("\n Smoothed level computed using the weights = ",
sum(y*as.numeric(wts$WtT),na.rm = T),
" \n Smoothed level from the Kalman Filter = ",fit_ks$ahatt[50])
#>
#> Smoothed level computed using the weights = 834.9828
#> Smoothed level from the Kalman Filter = 834.9828cat("\n Filtered level computed using the weights = ",
sum(y*as.numeric(wts$Wt),na.rm = T),
" \n Filtered level from the Kalman Filter = ",fit_kf$att[50])
#>
#> Filtered level computed using the weights = 849.307
#> Filtered level from the Kalman Filter = 849.307In this example we show how to compute observation weights for a Dynamic Factor Model (DFM) which are then used to decompose the latent factor into the contribution of each variable.
More formally, let \(x_{t}=(x_{1,t},x_{2,t},...,x_{n,t})^{\prime}\) with \(t =1,2,...,T\) be a vector of \(n\) monthly series that have been transformed to become stationary and standardized. A dynamic factor model (DFM) assumes that it is possible to decompose \(x_{t}\) into two unobserved orthogonal components representing common and idiosyncratic factors. The model is specified as follows:
$$
x_{t}=\Lambda F_{t}+\varepsilon_{t}, \hspace{2pt} \varepsilon_{t}\sim N(0,R),
$$where \(F_{t}\) is an \((r \times 1)\) vector of unobserved common factors, \(\Lambda\) is an \((n \times r)\) matrix of their loadings, and \(\varepsilon_{t}\) is an \((n \times 1)\) vector of the idiosyncratic components. The factors are assumed to have the following stationary VAR(p) representation:
$$
F_{t}=\sum_{s=1}^{p}\Phi _{s}F_{t-s}+u_{t},\hspace{2pt} u_{t}\sim N(0,Q)
$$where \(\Phi_{s}\) are \((r \times r)\) matrices of autoregressive coefficients. The related inference and forecast procedures can be carried out using the standard Kalman filter techniques.
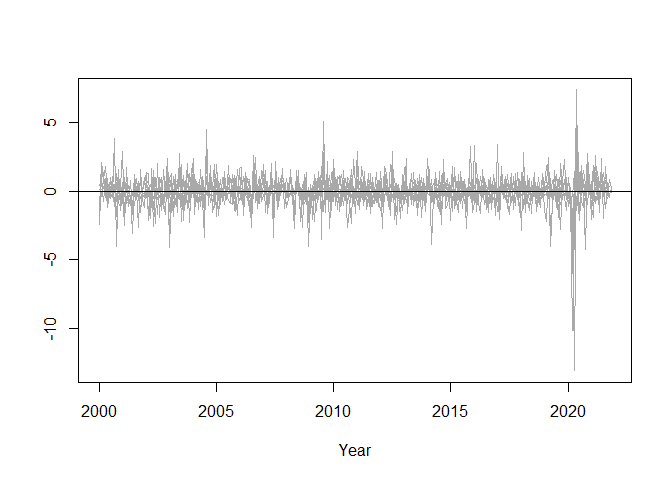
In this illustrative example, we use a dataset containing 10 monthly economic indicators covering the period from January 2000 to November 2021. All variables have been log-differenced, when necessary, to achieve stationarity. We assume that there is a single laten factor that follows an AR(1) process.
The normalized data series are summarized in the plot below:
Below, we use the wex function to decompose the last
value of the latent factor into a contribution of each variable.
# defining the stat-space matrices
Zt <- matrix(c(0.37873307, 0.37438154, 0.37767322,
0.02433999, 0.36020426, 0.23031769,
0.36584474, 0.35066644, 0.33420247,
0.01379571),
ncol=1
)
Tt <- matrix(-0.3676422)
HHt <- matrix(1)
GGt <- matrix(c(
0.7891011, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0.3235747, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0.7673983, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0.01704776, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0.9979156, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0.8496217, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0.8132641, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0.9084006, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0.7601053, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0.1789897
), nrow = 10, ncol = 10, byrow = TRUE)
# Extracting weights for the last obseravtion
wts <- wex(Tt=Tt,
Zt=Zt,
HHt = HHt,
GGt = GGt,
yt = t(df),
t=nrow(df))
# Computing contributions
ctr <- matrix(0,nrow=nrow(df),ncol=ncol(df))
for (i in 1:nrow(df)) {
ctr[i,]=as.numeric(wts$WtT[,,i]*df[i,])
}
ctr <- data.frame(ctr)
colnames(ctr) <-colnames(df)
contributions <- colSums(ctr,na.rm=T)The contributons are summarized in the Table below:
| Variable | Contribution |
|---|---|
| Total industrial production in Israel | 0.044 |
| Trade revenue | 0.065 |
| Service revenue | -0.023 |
| Employment (excluding absent workers) | 0.060 |
| Exports of services | 0.010 |
| Building starts | 0.001 |
| Imports of consumer goods | 0.019 |
| Imports of production inputs | 0.010 |
| Exports of goods | 0.003 |
| Job openings | -0.002 |
| Total | 0.188 |
Koopman, S. J., & Harvey, A. (2003). Computing observation weights for signal extraction and filtering. Journal of Economic Dynamics and Control, 27(7), 1317-1333.
The views expressed here are solely of the author and do not necessarily represent the views of the Bank of Israel.
Please note that wex is still under development and may
contain bugs or other issues that have not yet been resolved. While we
have made every effort to ensure that the package is functional and
reliable, we cannot guarantee its performance in all situations.
We strongly advise that you regularly check for updates and install any new versions that become available, as these may contain important bug fixes and other improvements. By using this package, you acknowledge and accept that it is provided on an “as is” basis, and that we make no warranties or representations regarding its suitability for your specific needs or purposes.